Se llaman curvas cónicas a las curvas que se obtienen de la intersección de una superficie cónica por un plano.
Secciones de un cono
Supongamos un cono de revolución de dos ramas; según sea la posición de un plano secante respecto del eje del cono, en relación con el ángulo del vértice, se obtienen las siguientes curvas:
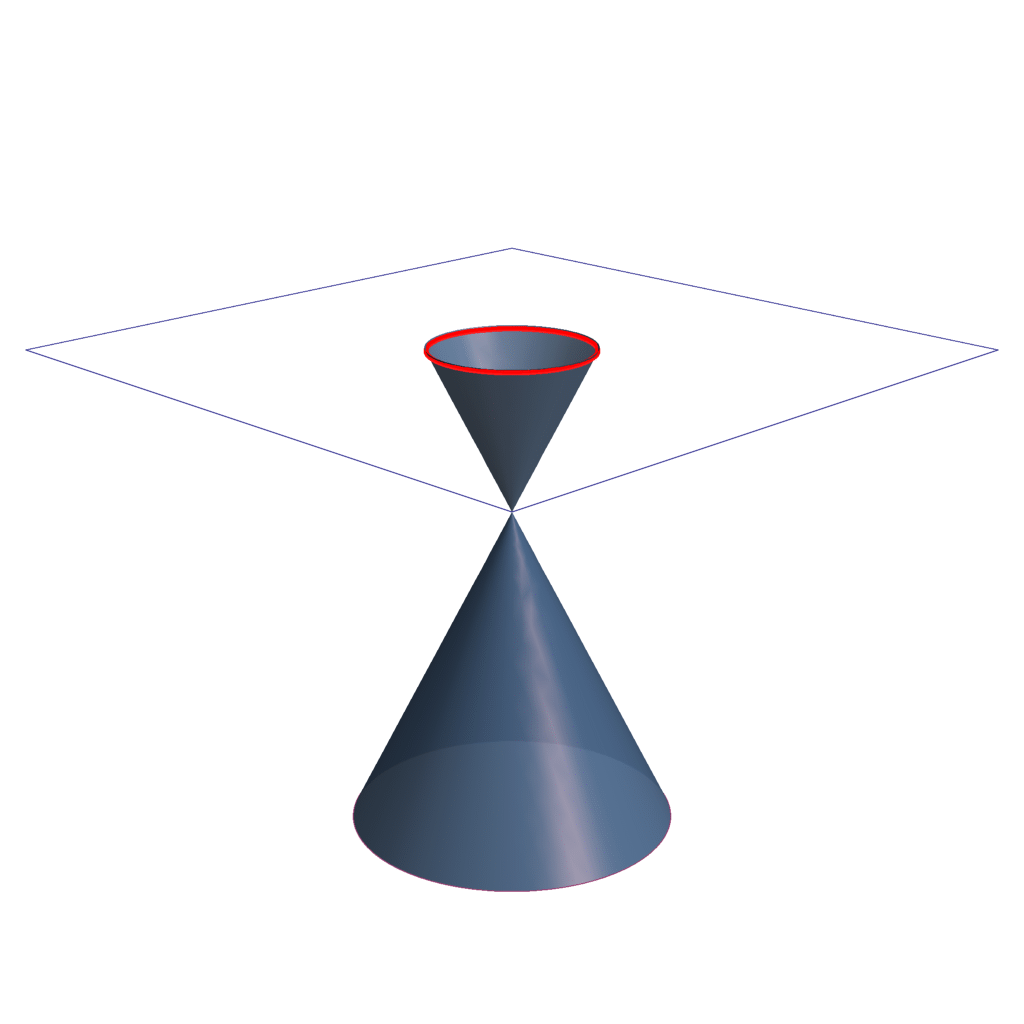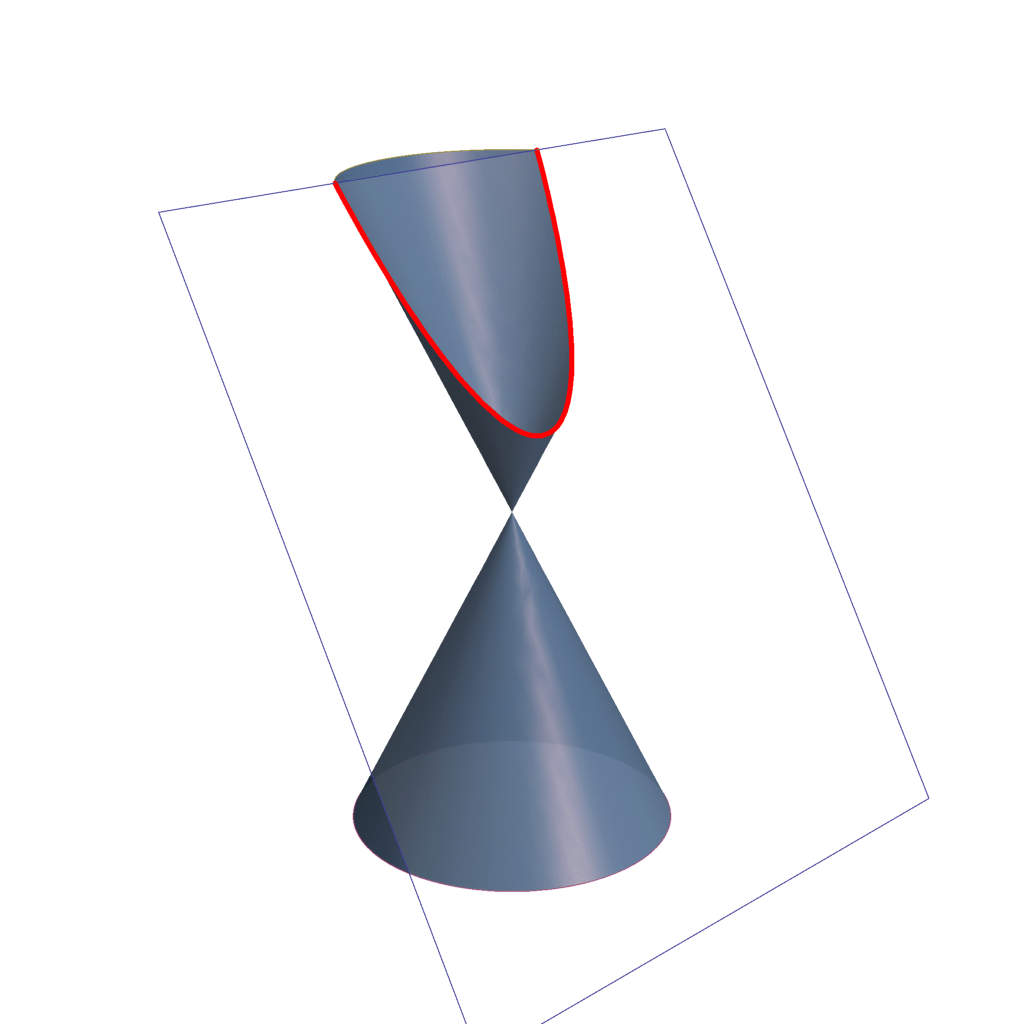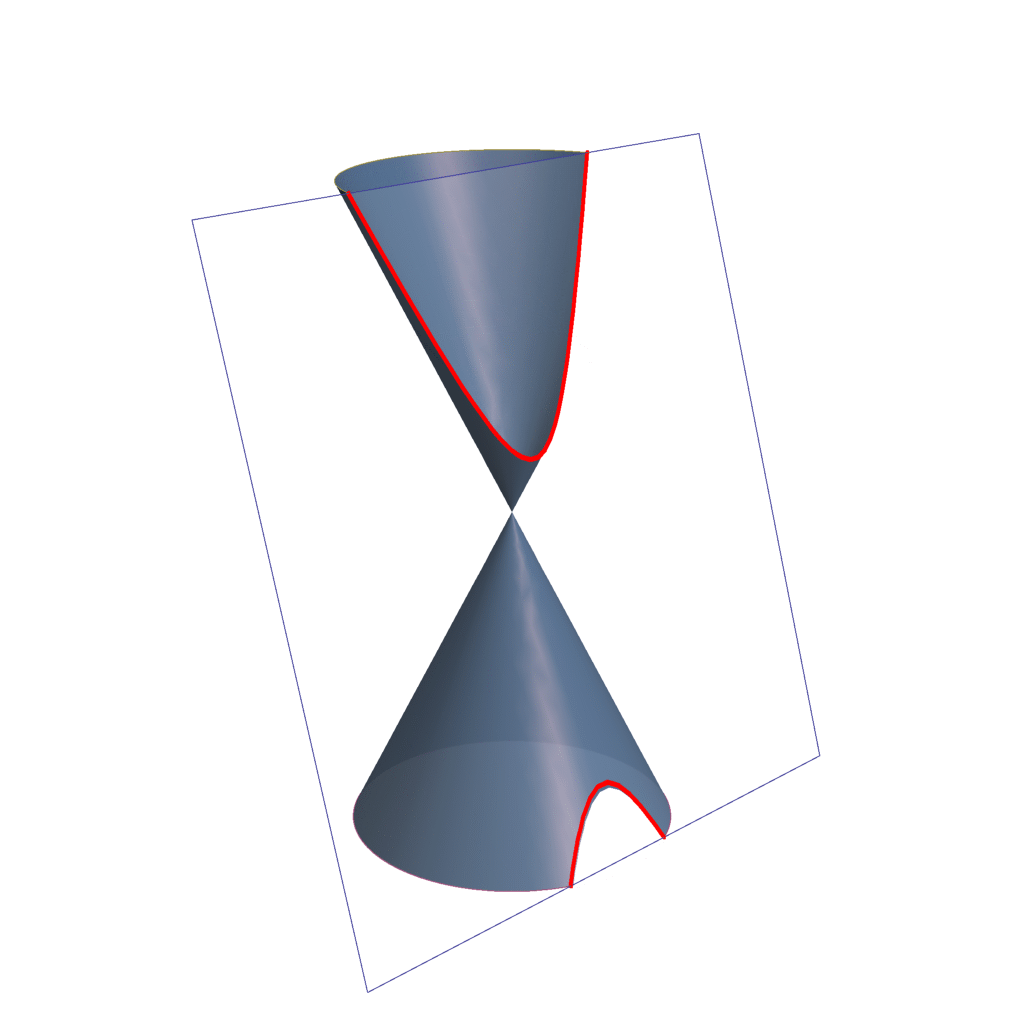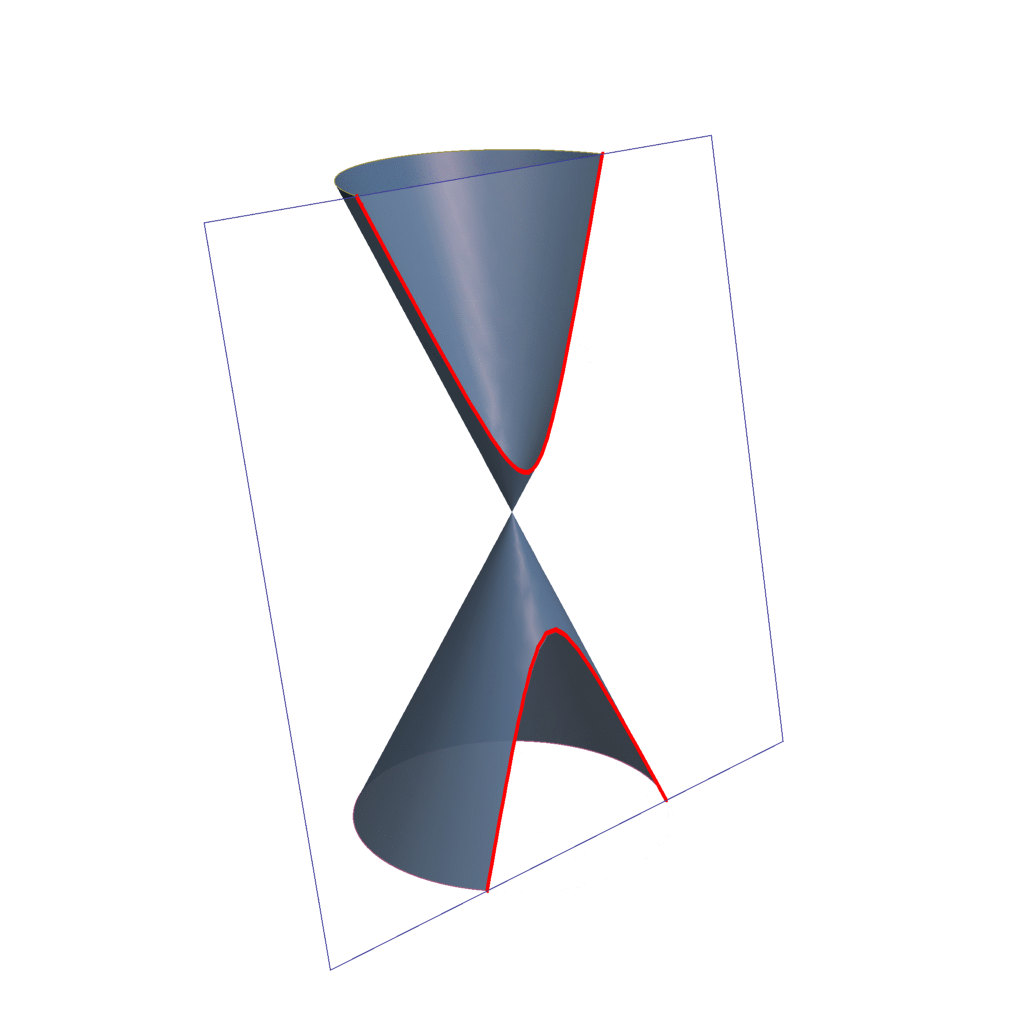
- Circunferencia
- Cuando el plano secante es perpendicular al eje de la superficie cónica, y no pasa por el vértice, la sección es una circunferencia. (α = 90º)
- Elipse
- Si el plano secante forma con el eje de la superficie cónica un ángulo mayor que semiángulo en el vértice del cono, el plano corta a todas las generatrices y no pasa por el vértice, entonces la sección es una curva cerrada que se denomina elipse. (α > β)
- Parábola
- Si el plano secante forma con el eje del cono el mismo ángulo que el semiángulo en el vértice o , lo que es lo mismo, es paralelo a una generatriz, la curva que resulta es abierta con un punto en el infinito llamada parábola (α = β).
- Hipérbola
- Cuando el plano secante forma con el eje del cono un ángulo menor que semiángulo en el vértice, entonces el plano corta a las dos ramas del cono y la sección es una curva abierta de dos ramas que se llama hipérbola. (α < β).
Clicar sobre el dibujo para comenzar/detener la animación. Ver dibujo en la página de Monnge.